CED2 - Why is current produced to a wire when moving a magnet close to it?
this answer provided by /u/Aliudnomen
charged particles moving in a magnetic field experience a force called the Lorentz force, given by
\[\vec{F}_L = q(\vec v \times \vec B)\]
With \(q\) the charge of the particle. The cross product means that the force is perpendicular to both the velocity (\(\vec v\)) and the magnetic field lines (\(\vec B\)).
When you move the magnet close to the wire, you're essentially creating this situation,
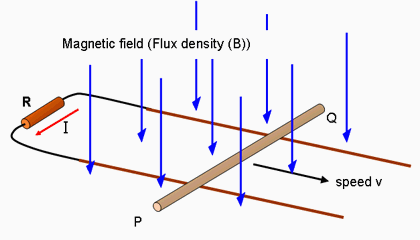
quite the situation
only in this case it's the magnetic field that is 'moving' (actually changing). The movement of the bar PQ in the linked image causes a force on the charged particles inside it, from the right hand rule this force acts from P to Q for positively charged particles and from Q to P for negative ones.
If we go a little deeper, we find that we can express the force per unit charge as
\[f = \vec{v} \times \vec{B}\]
Taking the line integral of this gives us the electromotive force that the magnetic field exerts on the charges in the wire:
\[\text{emf} = \int_\text{wire} \vec{f} \cdot d\vec{r}\]
This electromotive force acts as a voltage, so you end up getting a current through your wire! The above is nicely summarized in Faraday's Law of Induction, one of Maxwell's famous equations:
\(\nabla \times E = -\frac{\partial B}{\partial t}\)
Read: a changing magnetic field (such as when you move a magnet near a wire) induces an electric field.